同時，不少影音愛好者及發燒友也同樣希望能夠了解此類內容。因此，“影音新生活”開設特別專題，綜合全面地介紹音響學基礎知識，幫助大家更方便地了解聲學及音響技術。
只要不是自幼失聰者，對聲音都會有一個具體概念。但就大多數人來說，聲音的物理特性卻是陌生的。下面就為大家簡單講解一下聲音是如何產生和傳播的。
▌ 振動與頻率
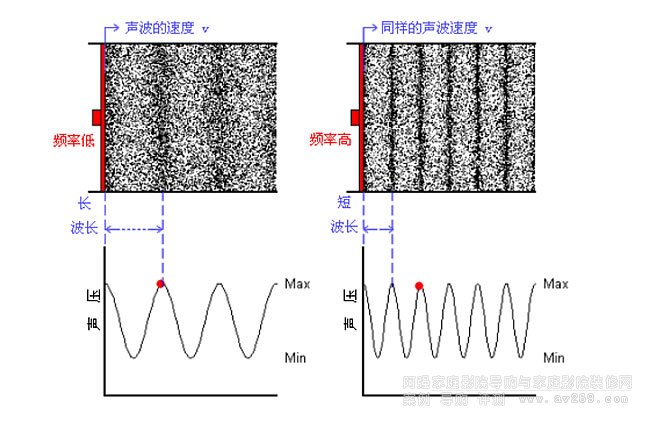
物體在外力影響下，沿著直線或曲線并經過其平衡位置所作的往返運動，稱為振動。振動體往返振動一次，稱作一個全振動過程。振動體在毎秒鐘完成的全振動次數，稱為頻率，常用單位稱為赫茲，簡稱赫（Hz)。10次/秒即l0Hz，1000次/秒即1KHz。頻率的高低決定于振助的快慢，每秒鐘振動的次數越多，頻率越高，反之亦然。我們日常所習慣的“高頻音”、“低頻音”的稱呼，是個相對的概念。高頻大約為1kHz以上的聲音，低頻大約為440Hz以下的聲音。
▌ 聲波與波速
物體的振動，會以一定的速度在媒介質（如固體、氣體、液體）內傳播開來。這種傳播過程，稱為聲波擴散。聲波傳播速度因媒介質密度不同而異。例如在15℃的空氣中聲音的速度每秒鐘344m(米），在水中每秒鐘l437m，在顱骨中每秒鐘3013m。
▌ 振幅與衰減振動
物體在振動過程中偏離平衡位置時的最大值，稱為振幅。振幅的大小決定于使物體振動的外力。在彈性限度內，外力越大，振幅也越大。物體在振動過程中，因克服磨擦和自身彈性所產生的阻力，造成能量損失，而使振幅隨時間逐漸減小直至消失，這是振動的衰減現象。絕大多數物質的振動都存在衰減現象，只有在能量得到補充的情況下，振動才能持續。聲音的大小同振幅的大小有關。
▌ 振動曲線、正弦波、波長
用圖形的方法來描述振動或波動狀態的圖像，稱為振動曲線或波動曲線。在現代條件下，這種曲線通常使用儀器來獲得。
振動曲線如果隨時間按三角函數正弦的規律變化的，稱為簡諧振動，其波形為正弦波。正弦波是一切振動中最基本的波型，輕輕敲擊音叉時產生的振動，就屬于這種類型。
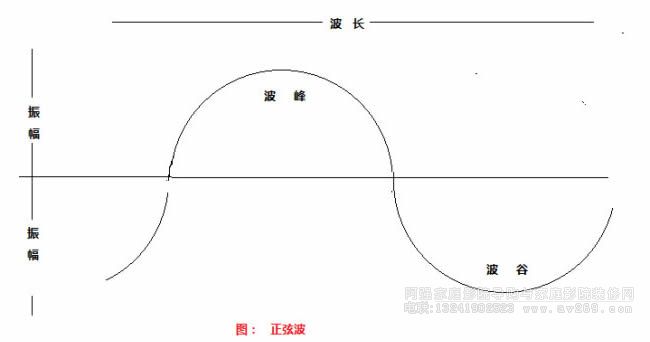正弦波凸起的最高點，稱作波峰；凹下去的最低點，稱作波谷。圖中橫軸自左至右代表的傳播方向，波峰或波谷至橫軸之間的距離表示振幅。橫軸上從平衡位置出發每經過一次波一次波谷再回到平衡位置，代表波長。不同頻率的聲波，其波長也不同，頻率越高，波長越短，頻率同波長的計算方式：V/f=h，其中：f=頻率，V=波速344m/s，h=波長，例如200Hz的波長為1.72m。波長不同對人耳辨別聲音位置影響很大。
▌ 位移、相位、相位差
振動體在振動過程中，或者媒介質在聲波傳播的過程中所發生的位置的移動，稱為位移。用來表示振動（波動）在某一時刻位移狀態的一個量稱為相位。這個量通常用角度來表示，稱為相位角，簡稱相。
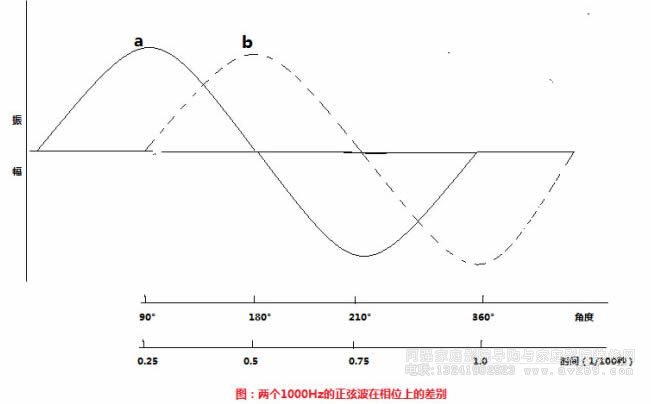
振動體處于平衡位置（即未發生振動時的位置）時，相位角一般處于0，如果是簡諧振動，當位移達到最大值時，相位角為90°或270°，相位相同之點，稱作同相點；相位相反之點，稱作反相點。例如兩個頻率一致的音叉，如果同時被擊會產生完全一致的振動，它們的聲波相位也完全一致。如果擊動的時間有先后，那么兩個音叉所產生的聲波就會出現相位差。上圖是兩個l000HZ的正弦波。這兩個正弦波在時間上相差1/4周期，當b波開始時，a波的振幅已達到最大值，當b波振幅達到最大值時，a波走到平衡位置。因此，兩波的相位差為90°
聲波的相位差對聽覺的響度感、方位感有重要影響。
▌ 受迫振動與共振
一件物體受到外力后發生振動，在外力突然消除后，由于物體自身內部的彈性作用而繼續進行振動，這種振動稱為自由振動，自由振動的頻率稱為固有頻率。A物體的自由振動，激起B物體也按A的頻率來振動，這時，B的振動稱為受迫振動，或稱強迫振動。例如在提琴上撥弦后琴弦自身按其固有頻率產生自由振動，當琴弦的自由振動通過琴馬傳輸給提琴的共鳴箱，引起共鳴箱按琴弦的頻率來振動，這時，共鳴箱的振動就是受迫振動。
實驗證明，自由振動的頻率如果同受迫振動體的固有頻率相一致或十分接近時，振幅（音量）會迅速達到它可能的最大值。這種現象叫做共振，又稱諧振，在聲學上就叫做共鳴。其音響稱共鳴音。當然，我們還要注意到：如果自由振動的頻率同受迫振動體的固有頻率很不一致，則振幅減小甚至失音。
▌ 耦合
耦合是共振的另一種屬性。當兩個或兩個以上的振動體系通過共振作用而彼此聯合起來時，會產生出一種新的振動體系，這種物理現象稱為耦合，耦合是許多管樂器的發聲原理。例如雙簧管是依靠哨子的振動來發聲的，但單吹哨子時，不僅頻率不準確，而且音色也不美，然而當哨子同樂器的管身連接在一起時，音色馬上好聽起來。這就是因為哨子（簧振動)同共鳴管（空氣柱）振動發生耦合的緣故。結合音效應也是耦合的一種類型。在一定條件下，兩個不同頻率的合成波的迭加（例如樂器合奏），會出現第三個不同頻率的聲音。此外，自然沉音的產生，亦同耦合現象有關。
在聽音過程中，人耳亦會產生耦合的現象，對生理和心理會產生影響。
▌ 波的合成
兩個或多個波重疊在一起時，稱作迭加，迭加后形成新的波稱為合成波。多個不同頻率、不同相位、不同振幅的波的迭加，可以產生很復雜的合成現象。
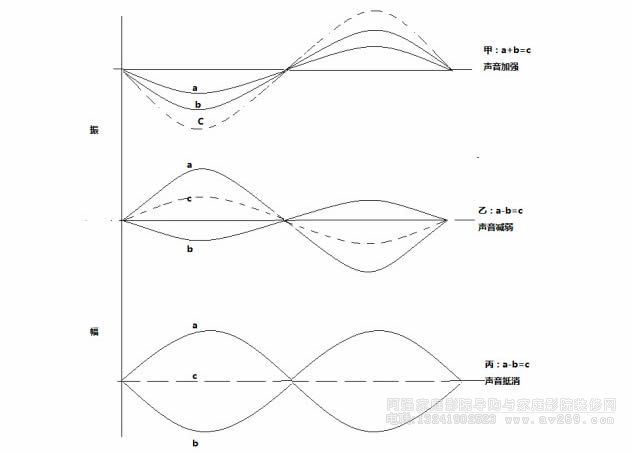列舉三種最簡單的合成波現象，如上圖，迭加前的波用實線表示，合成波用點線表示。圖中甲：a波與b振幅不同，相位相同，迭加后聲音加強。乙:a波與b波振幅不同，相位相反，迭加后聲音減弱。丙：a波與b波振幅相同相位相反，迭加后聲音抵消。波的迭加在音色、音量及結合音的心理感覺方面，均起關鍵作用。
▌ 拍音
如果兩個波的頻率不同但相近，合成后的振幅就會發生周期性改變的現象，稱為拍。由聲波合成后所出現的拍的音響，稱為拍音。圖13-4是A、 B兩波及合成后的波型。圖中 A+B合成后振幅毎秒鐘的周期變化次數稱為拍頻，它等于兩波頻率的差。
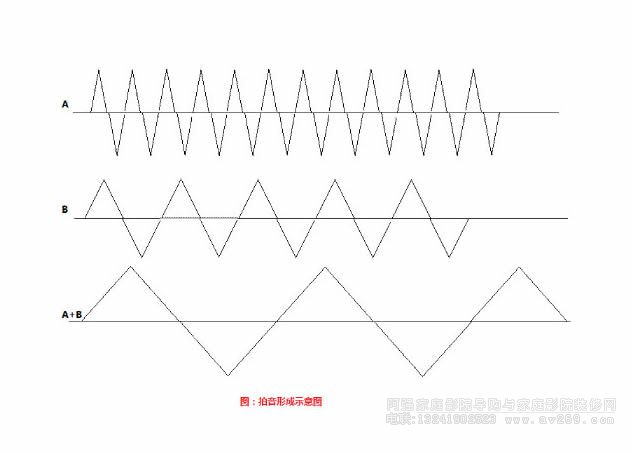
如圖所示，若A波為50Hz，B波為40Hz，合成后50—40=10(Hz)， 拍頻為l0Hz/s。 拍頻是兩個波互相干涉的現象。拍音現象常用來給樂器（如鋼琴）調音：當樂器兩個音頻率有微小差別時會聽到拍音，拍音消失時證明音高統一。此外，一些樂器（如口琴、手風琴、風琴等）則有意制造拍音現象，使發聲波動而達到美化音色的目的。
小結：掌握聲音傳播的基礎知識，能夠更好地幫助我們去了解音響產品、室內建筑的聲學特性，有利于打造優秀的視聽環境。
